Query Language
MPC provides a general way of computing a function by several parties potentially allowing any computation. However, not all the computations are feasible to use in practice due to performance considerations. The query language exposes carefully chosen functions for statistical analysis. More functions can be added to the language depending on use cases and after the detailed performance cost estimation.
A single analysis may include one or more calculations (queries). Each query consists of a filter expression and one or more functions that are applied to the input data after filtering.
Example
| age | salary |
|---|---|
| 20 | 10000 |
| 18 | 12000 |
| 78 | 9900 |
| 67 | 15000 |
Compute the average salary for all employees older than 25
Filter: age > 25 Result: 2/4 (2 of 4 rows)
Function: mean(salary) Result: 12450
This document uses variable to correspond to the name of a column in a dataset.
Filter expressions
A filter expression consists of one or more comparison expressions connected with logical AND and OR operators. A filter expression can also be negated using logical NOT.
Each comparison expression consists of a variable (a column from the data set), a comparison operation and a value to compare the variable to.
| Operations | Symbols |
| ---------: | -------------------------------: | --------------- |
| Comparison | <, >, <=, >=, ==, != |
| Logical | & (AND), |(OR),! (NOT) |
Example
Find all employees with a salary between 10000 and 20000 or younger than 30.
(salary => 10000 & salary <= 20000) | age < 30
Find all employees with a salary outside the interval between 10000 and 20000 (note the negation operation !)
!(salary => 10000 & salary <= 20000)
Functions
min(variable)
Compute minimum of all values of variable.
Arguments:
- a variable corresponding to a column name
Example: min(age) = 18, for the example dataset
The min function reveals the exact value of a single data point in the data set. Whether to use this function should be determined on a case-by-case basis.
max(variable)
Compute maximum of all values of variable.
Arguments:
- a variable corresponding to a column name
Example: max(age) = 78, for the example dataset
The max function reveals the exact value of a single data point in the data set. Whether to use this function should be determined on a case-by-case basis.
mean(variable)
Compute the sample mean (the average value).
Arguments:
- a variable corresponding to a column name
Example: mean(salary) = 11725, for the example dataset
variance(variable)
Compute the sample variance. The variance characterizes the average degree to which each point differs from the mean.
Arguments:
- a variable corresponding to a column name
Example: variance(age) ≈ 974.9167, for the example dataset
standardDeviation(variable)
Compute the sample standard deviation as the square root of the sample variance. The standard deviation characterizes how far values are spread out from the mean (average value).
Arguments:
- a variable corresponding to a column name
Example: standardDeviation(age) ≈ 31.2237, for the example dataset
sum(variable)
Compute the sum of all values of the given variable.
Arguments:
- a variable corresponding to a column name
Example: sum(salary) = 46900, for the example dataset
prevalence(filter)
Compute prevalence. Prevalence is the percentage of the dataset matching the filter criteria.
Arguments:
- A filter expression, e.g. age > 70
Example: prevalence(age > 70) = 25%, for the example dataset
count()
Compute number of rows after applying a filter expression.
Arguments: none
Example: filtering the example dataset with age > 18 and then computing count() gives 3.
chiTest(variable, [NUM], [INT])
Compute Chi-square test.
Chi-square (χ²) test is used to test whether the observed data corresponds to some expected data. E.g. observations correspond to some theoretical probability distribution, or two observed variables are independent of each other (for example, the fact that people buy snacks or not is independent of the type of the movie they attend).
Arguments:
- a variable corresponding to a column name
- a list of numbers (possibly decimals) corresponding to histogram buckets
- a list of integers corresponding to expected values for each bucket
histogram(variable, [INT])
Compute a one-dimensional histogram.
Arguments:
- a variable corresponding to a column name
- a list of integers - soft (less-or-equal) - upper bounds of the histogram buckets.
Output: count of elements in each bucket; the last count corresponds to the elements larger than the last bound in the input list of bounds. Note that the count for any of the buckets is below k (the anonymity threshold), the whole result is <k, and it is not possible to see for which bucket the count was below the threshold.
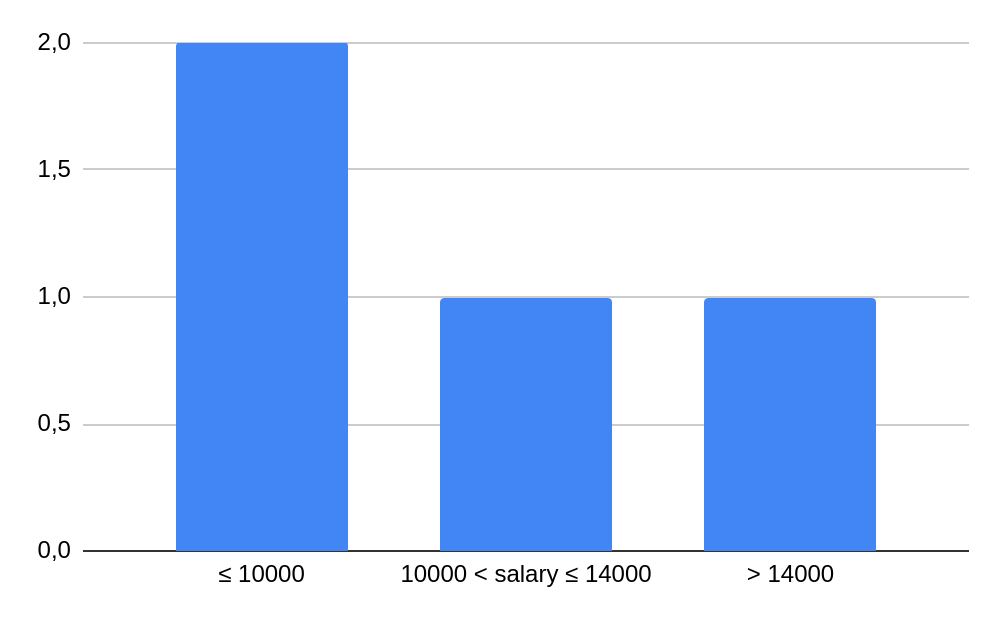
Example: histogram(salary, [10000, 14000]) = [2, 1, 1], for the example dataset. The buckets: salary ≤ 10000, 10000 < salary ≤ 14000, salary > 14000. The histogram can be visualized in the following way:
tTest(variable, NUM)
Compute the test statistics for a Student's t-test for the hypothesis that the mean (average) of the sample is equal to the given value. For example, one can test a hypothesis that, on average, protein bars have 20 grams of protein.
Arguments:
- a variable corresponding to a column name
- a number (possibly decimal) corresponding to the
Lists are written as comma-separated numbers in square brackets, e.g: [1,2,3.6]